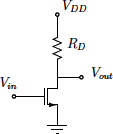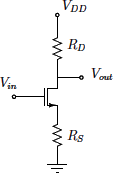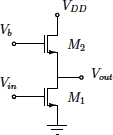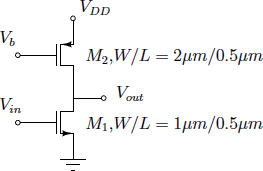Common Data : V_DD = 1.8V , L_min  = 0.18µm, µ_0N = 350cm²/V s, µ_0P  = 100cm²/V s, |V_TH | = 0.55, t_ox = 3.8nm, λ = 0.07V⁻¹, χ = 0.1.

For the curved surface of the cylinder, the unit vector is which gives  Parameterize ,Since we are confined to the first octant The flux through the slant surface is .  The top and the bottom caps are in the  directions, the contribution from these two give zero by symmetry.  There are two more surfaces if we consider the first octant, they are the positive x-z plane and the positive y-z plane., the normal to the former being in the direction of  while that for the latter is along  directions. The flux from the former is , while that from the latter is .  Adding up all the contributions, the total flux from the closed surface is zero. This is consistent with the fact that the divergence of the field is zero.

1. For a MOSFET operating in the linear (triode) region (ignore body effect and channel- length modulation), find an expression for:

1. the small-signal transconductance g_m
2. the small-signal drain-source output resistance r_out

Comment upon your findings.  Is it desirable for an amplifier to work in the linear region? Explain.

2. Consider the simple MOS amplifier shown in Figure 2. Assume λ = 0 and V_DD = 1.8V.

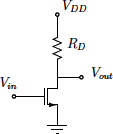
Figure .2

Assume that the biasing for the gate side of the MOS is taken care of.

1. For maximum symmetrical swing in Vout  and for a drain current of 0.8 mA, find the required value of R_D .
2. Calculate the maximum symmetrical output swing, and also the small-signal volt- age gain in this case.
3. How would the design values and the voltage gain change, if λ = 0.07 V⁻¹?

3. Consider the circuit in Figure 3.

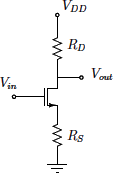
Figure. 3 Circuit for Q3

If I_D = 0.5mA, R_D = 1.5kΩ and R_S = 300Ω, calculate:

1. the small-signal voltage gain
2. the input voltage which will place the NMOS on the border of linear/saturation region, assuming γ = λ = 0. What would be voltage gain under this condition?

The divergence of the field is 3. The flux, therefore, is  3 times the volume of the cone which is The flux is thus  The  direct calculation of the flux involves two surfaces, the slant surface and the cap, as shown in the figure. The cap is in the xy plane and has an outward normal . The flux (because on the cap z=1 and the cap is a disk of unit radius).  Thus it remains to be shown that the flux from the slanted surface vanishes. At any height z, the section parallel to the cap is a circle of radius z. Since, the height and the radius of the cap are 1 each, the semi angle of the cone is 45⁰.

Thus the normal to the slanted surface has a component  along the z direction and  in the x-y plane. The component in the xy plane can be parameterized by the azimuthal angle  and we can write  . The area element can be written as  , the factor  appears because the length element is along the slant. Thus the contribution from the slanted surface is  . Using  , this integral can be evaluated and shown to be zero.

4.Consider the circuit shown in Figure 4. Assume V_DD = 1.8V . The amplifier has to be designed such that I_D = 100 µA.

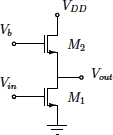
Figure. 4 Circuit for Q4

1. What should be the bias voltage Vb  for the required I_D ?
2. What are the maximum and minimum values of V_out required to keep both M₁ and M₂ in saturation?
3. Calculate the small-signal voltage gain offered by this circuit .

This problem is to be attempted similar to the problem  5 of the tutorial, i.e., by closing the cap and subtracting the contribution due to the cap. The divergence being 3, the  flux from the closed cone is 3 times the volume of the cone which gives   The contribution from the top face (which is a disk of  radius 2 ) is . Thus the net flux is zero.  (You can also try to get this result directly as done in problem 4, where we showed that the flux from the curved surface is zero).

5. Consider the circuit shown in Figure 5.

Figure. 5 Circuit for Q5

1. What are the maximum and minimum values of V_out required to keep both M₁ and M₂ in saturation?
2. Obtain an expression for the small-signal voltage gain offered by this circuit.

6. Consider the circuit in Figure 6. Assume V_DD = 1.8 V.

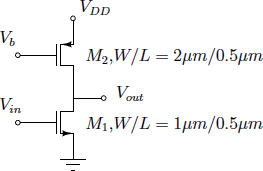
Figure. 6 Circuit for Q6

1. What should be the bias voltage V_b  if this amplifier is to provide a small-signal voltage gain of 25 ?
2. What are the maximum and minimum values of V_out required to keep both M₁ and M₂ in saturation ?
3. How would the voltage gain change if M₂ were replaced by an ideal current source that provides the same current as required in part (a)?

1. Since M₂  is a current-source load, it should be in saturation.  Also, M₁  should be in saturation. The small-signal gain of the circuit is thus given by

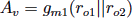
Since the λ of both transistors are equal, we have r_o1 = r_o2 = r_o. Thus,

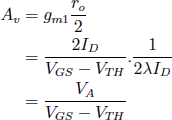
Substituting the values, we find, V_GS − V_TH  = 0.57V. Thus, the current through M₁ is approximately 0.2mA. The same current should flow through M₂ as well. So we obtain the V_GS for M₂ to be approx. -1 V. Thus, V_b = V_DD − V_SG = 0.8 V.

2. For M₂ to be in saturation, we need V_DS < V_GS − V_TH , i.e V_out − V_DD < −0.45 ⇒ V_out < 1.35 V. Thus, the maximum allowed V_out is 1.35 V. For M₁ , we need V_out > V_GS − V_TH ⇒ V_out > 0.57V. Thus, the minimum allowed V_out is 0.57V.

3. An ideal current source would have an infinite resistance. Thus, there would be no r_o2  as offered by M₂. The gain expression would thus have reduced to A_v  = g_mr_o, hence for the same current as in part (a), the gain would now be 25 × 2 = 50 .